如果结果不匹配，请 
更多“在一元线性回归模型y=β0+β1x+ε中，属于随机变量的是(…”相关的问题
第1题
如果对一个简单的线性回归模型进行显著性检验时，如y=β0+β1x+μ，则备择假设为（)。
A.H0:β0=β1=0，并运用F检验
B.H0:β1=0，并运用F检验
C.H0:β1=0，运用T检验
D.B和C都是正确的，可以仍选其一进行检验
第2题
在简单线性回归模型y=β0+β1x+u中，假定E(u)≠0。令α0=E(u)，证明：这个模型总可以改写
在简单线性回归模型y=β0+β1x+u中，假定E（u)≠0。令α0=E（u)，证明：这个模型总可以改写
点击查看答案
为另一种形式：斜率与原来相同，但截距和误差有所不同，并且新的误差期望值为零。
第4题
以下关于一元线性回归叙述正确的有（)？
A.一元线性回归预测是回归预测的基础，预测对象只受一个主要因素影响
B.判定一个线性回归方程的拟合程度的优劣称为模型的显著性检验，通常用的检验法是相关系数检验法
C.相关系数等于回归平方和在总平方和中所占的比率，即回归方程所能解释的因变量变异性的百分比，是一元回归模型中用来衡量两个变量之间相关程度的判定指标
D.如果相关系数r=0，表示所有的观测值全部落在回归直线上;如果r=1，则表示自变量与因变量无线性关系
第5题
线性回归中，检验回归模型的F统计量，通常与给定的F临界值做比较，这里与F相比较的临界值取为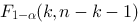
,如果是一元线性回归，则临界值直接取为
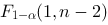,这里的参数
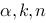的含义为：
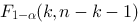,如果是一元线性回归，则临界值直接取为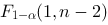,这里的参数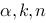的含义为：A.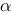
为显著性水平，k为回归模型中自变量的个数，n为样本容量
B.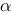为显著性水平，k为样本容量，n为回归模型中自变量的个数
C.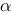为显著性水平，k为回归模型中自变量的次数，n为样本容量
D.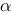为显著性水平，k为回归模型中自变量的个数，n为回归模型中自变量的次数
第6题
如果两个变量之间存在线性关系，其中一个是自变量，另一个是因变量利用样本数据，建立他们之间关系的数学模型，对模型进行统计检验，并利用这—模型进行预测和控制，就是（)。
A.二元线性回归
B.二元二次线性回归
C.多元线性回归
D.一元线性回归
第7题
对于线性回归模型Yi=0+β1Xi+Ui，有关的β1方差的估计量的说法错误的是（)。
A.残差平方和越大，β1的方差的估计量越大
B.样本容量越大，β1的方差的估计量越小
C.Xi的方差越大，β1的方差的估计量越小
D.Xi的方差越大，β1的方差的估计量越大。
第9题
考虑简单回归模型 y=β0+β1x+u 令z为x的二值工具变量。运用教材（15.0)，证明Ⅳ估计量β
考虑简单回归模型
y=β0+β1x+u
令z为x的二值工具变量。运用教材(15.0)，证明Ⅳ估计量β1可以写成：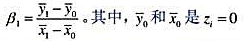
的那部分样本中yi和xi的样本平均值，而
的样本平均值。该估计量称为群组估计量，它是由沃德(Wald，1940)最先提出。
第11题
在高斯-马尔可夫假定SLR.1至SLR.5之下，考虑标准的简单回归模型y=β0+β1x+u.通常的OLS估
计量β0和β1都是各自总体参数的无偏估计量。令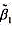
表示通过假定截距为零而得到的β1的估计量。
点击查看答案
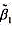表示通过假定截距为零而得到的β1的估计量。
